Standsicherheit einer Maschine berechnen

Der tragische Unfall mit einem Baukran zeigt, wie wichtig die Standsicherheit von technischen Anlagen ist. In diesem Artikel möchten wir Ihnen an einem einfachen Beispiel zeigen, wie man die Standsicherheit einer Maschine berechnet.
Dieser Artikel beschäftigt sich mit den Grundlagen der Standsicherheit und versucht die Berechnung des Standsicherheitsfaktors an einem möglichst simplen Beispiel zu erläutern. Die vereinfachte Berechnungsform findet man oftmals im Grundlagenstudium vieler Hochschulen, wo sie für nahezu alle Maschinentypen eingesetzt wird.
Möchten Sie über die theoretische Betrachtung der Standsicherheit hinausgehen und beispielsweise eine Maschine produzieren und in den Verkehr bringen, reicht diese Form des Standsicherheitsnachweises nichts aus, da Sie in Europa die Vorgaben der Maschinenrichtlinie bzw. einer entsprechenden harmonisierten Norm erfüllen müssen.
Die DIN EN 280 liefert z. B. genaue Informationen für den Standsicherheitsnachweis einer fahrbaren Hubarbeitsbühne. Es werden unter anderem Vorgaben für anzusetzende Windlasten, Nutzlasten und zu berücksichtigende dynamische Kräfte gemacht.
Stand- und Kippmoment
Bevor wir Ihnen erklären können, wie die Standsicherheit einer Maschine beurteilt wird, müssen die Begriffe Stand- und Kippmoment bekannt sein.
Drehmoment
Ein Drehmoment ist das Produkt aus Kraft und Hebelarm. Je größer die Kraft oder je länger der Hebelarm, umso größer ist auch das Moment, welches auf das Bauteil wirkt.
Diesen Zusammenhang kann man leicht erkennen, wenn man mit einem Schraubenschlüssel eine Schraube lösen möchte. Sitzt diese Schraube fest, hat man zwei Möglichkeiten:
- Man muss stärker drücken, d. h. man vergrößert die Kraft.
- Man verlängert den Hebelarm, indem man einen längeren Schraubenschlüssel verwendet oder ein Rohr auf den Schlüssel setzt.
Standmoment
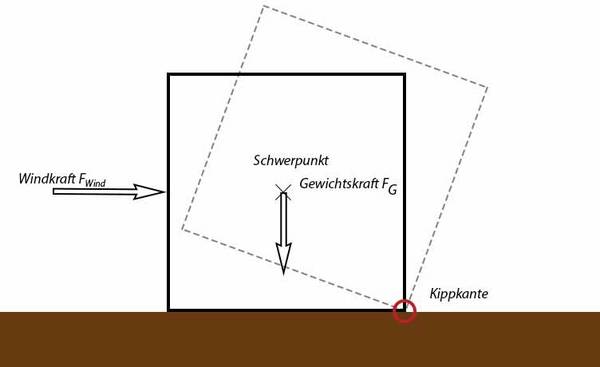
Als Standmoment bezeichnen wir die Summe aller Momente, die das Kippen der Maschine verhindern wollen. Diese Momente können beispielsweise durch das Kontergewicht oder das Eigengewicht der Maschine erzeugt werden. Ob das Eigengewicht zu den Kipp- oder zu den Standmomenten beiträgt, ist von der Lage der Kippkante und des Schwerpunkts abhängig - aber dazu später mehr.
Kippmoment
Als Kippmoment bezeichnen wir die Summe aller Momente, die die Maschine umkippen wollen. Erzeugt werden diese Momente beispielsweise durch den angreifenden Wind oder durch Lasten, die über die Kippkante hinausragen.
Berechnung der Standsicherheit
Eine Maschine steht immer dann sicher, wenn die Standmomente größer sind als die Kippmomente. Möchte man die Standsicherheit einer Maschine beurteilen, muss man folglich alle Kräfte betrachten, die die Maschine stabilisieren und die sie destabilisieren.
Um es möglichst einfach zu halten, möchten wir die Ermittlung der Standsicherheit an einem einfachen Würfel erklären.
Würfel auf einer geraden Fläche
Der Würfel verfügt über eine Kantenlänge von einem Meter, einer Masse von zehn Kilogramm und ist einem Winddruck von 70 N/m² ausgesetzt. Weiterhin gehen wir davon aus, dass die Dichte des Würfels homogen ist und der Schwerpunkt somit genau im Mittelpunkt des Würfels liegt.
Die nachfolgende Skizze fasst die Ausgangslage grafisch zusammen:
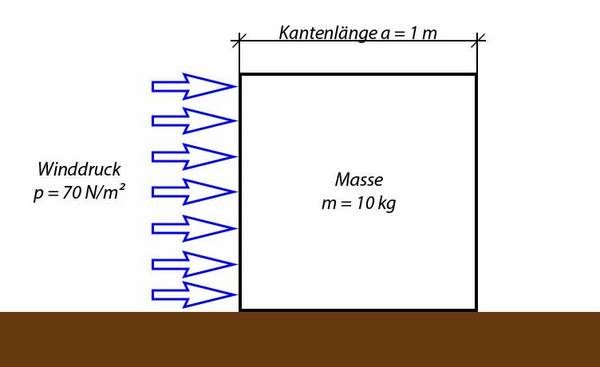
Gewichtskraft
Wie eingangs erklärt, brauchen wir zur Beurteilung der Standsicherheit Kräfte und Hebelarme. Daher müssen wir zunächst berechnen, wie groß die Kräfte sind und wo diese angreifen.
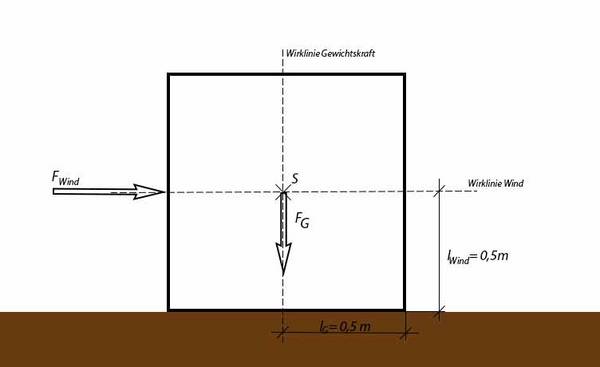
Da die Dichte des Würfels überall gleich (homogen) ist, befindet sich der Schwerpunkt genau im Mittelpunkt. Die Gewichtskraft greift immer am Schwerpunkt eines Körpers an und wirkt in Richtung des Erdmittelpunktes. Somit ist der erste Angriffspunkt bereits bekannt, allerdings fehlt noch die Höhe der Gewichtskraft. Diese lässt sich mit folgender Formel berechnen:
Windkraft
Nachdem die Gewichtskraft bekannt ist, stellt sich die Frage, wo die Windkraft angreift und wie hoch diese ist. In der obigen Skizze kann man gut erkennen, dass der Wind gleichmäßig auf die linke Seite des Würfels drückt. Anstelle der Flächenlast, die durch den Wind hervorgerufen wird, können wir daher auch eine große Kraft annehmen, die genau auf die Mitte der linken Fläche drückt. Der Angriffspunkt der Kraft ist somit bekannt.
Die Höhe der Kraft lässt sich leicht mit den Abmessungen des Würfels und dem gegebenen Winddruck berechnen. Die Windangriffsfläche des Würfels ist:
Somit ist die Windkraft:
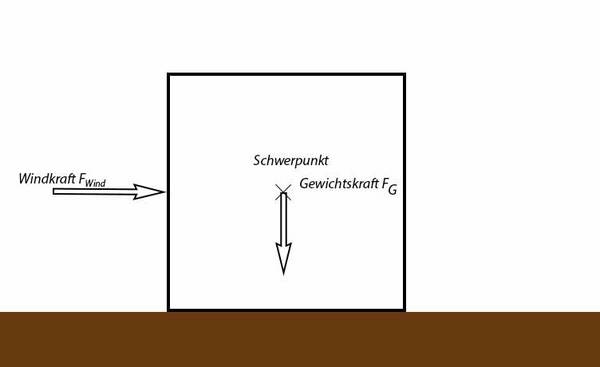
Die Skizze sieht jetzt wie folgt aus:
Von der Kraft zum Drehmoment
Da uns jetzt die Gewichts- und die Windkraft bekannt sind, stellt sich die Frage, welche Hebelarme relevant sind. Hierfür müssen wir wissen, wo die Kippkante der untersuchten Maschine bzw. in diesem Fall des Würfels liegt.
Diese Frage kann bereits durch einfaches Hinschauen beantwortet werden. Welche Kraft wird in unserem Beispiel versuchen, den Würfel umzukippen? Genau, die Windkraft. Wenn die Windkraft jetzt von links auf den Würfel drückt, über welche Kante wird der Würfel dann im schlimmsten Fall kippen? Richtig, über die rechte Kante.
Kräfte dürfen auf ihrer Wirkungslinie verschoben werden. Der Hebelarm ist der kürzeste Abstand zwischen der Wirkungslinie einer Kraft und der Kippkante. Wie der Zufall es möchte, beträgt der Hebelarm jeder Kraft genau eine halbe Kantenlänge.
Die Drehmomente lassen sich somit wie folgt berechnen:
Besteht Kippgefahr?
Wie zuvor bereits erwähnt, versucht der Wind den Würfel umzukippen. Die Gewichtskraft drückt den Würfel hingegen auf den Boden und wirkt somit der Windkraft entgegen.
Die Gewichtskraft erhöht also das Standmoment, während die Windkraft zum Kippmoment beiträgt. Da keine weiteren Kräfte und Momente vorliegen, bestimmen in diesem Beispiel nur die Windkraft und die Gewichtskraft über das Schicksal des Würfels. Das Moment der Gewichtskraft und somit das Standmoment ist größer als das Kippmoment aus der Windkraft. Somit besteht keine Gefahr, dass der Würfel kippt.
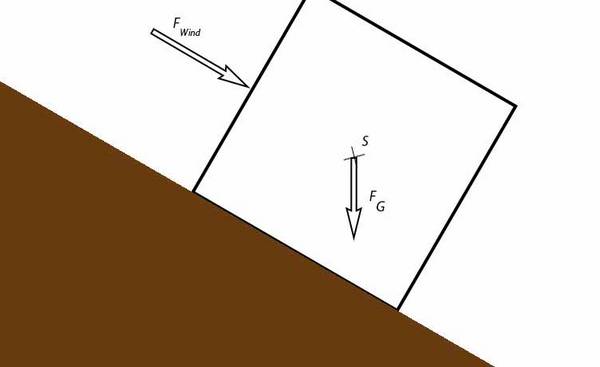
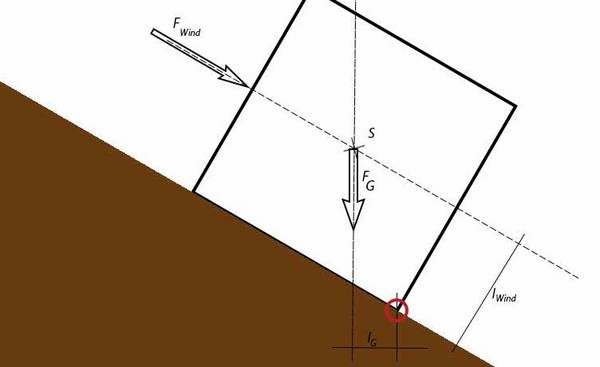
Würfel auf einer Rampe
Mit dem zweiten Beispiel möchten wir verdeutlichen, welchen Einfluss die Einsatzbedingungen einer Maschine auf die Standsicherheit haben. Der Würfel aus dem ersten Beispiel befindet sich jetzt nicht mehr auf einer ebenen Fläche, sondern auf einer 30°-Rampe. Im Alltag findet man diese Situation relativ häufig vor, z. B., wenn ein Fahrzeug an einer Böschung abgestellt wird.
Wir gehen davon aus, dass sich die Kräfte und Angriffspunkte nicht verändert haben und dieselben sind wie im ersten Beispiel. Daher finden wir nun folgende Situation vor:
Nachdem die Angriffspunkte der Kräfte bekannt sind, müssen erneut die Kippkante und die vorhandenen Hebelarme ermittelt werden. Zeichnet man in die Skizze die Wirkungslinien der Kräfte ein, so wird schnell deutlich, wieso eine Rampe oder Schräge die Kippgefahr erhöht.
Während sich der Hebelarm der Windkraft nicht geändert hat, ist der Hebelarm der Gewichtskraft wesentlich kleiner geworden. Wir wissen, dass die Gewichtskraft bisher das Kippen des Würfels verhindert hat. Da sich das Drehmoment proportional zum Hebelarm verhält, kann bereits jetzt gesagt werden, dass der Würfel auf der Schräge einer wesentlich höheren Kippgefahr ausgesetzt ist.
Die Berechnungen zeigen, dass im vorliegenden Fall folgende Drehmomente existieren:
Da das Kippmoment größer ist als das Standmoment würde der Würfel im vorliegenden Fall über die rechte Kante kippen. Im Falle eines Würfels ist dies sicherlich nicht tragisch. Handelt es sich dabei allerdings um ein Fahrzeug, dürfte sich niemand freuen.
Wird die Rampe steiler verstärkt sich dieser Effekt weiter. Ein besonderer Fall liegt vor, wenn die Wirkungslinie der Gewichtskraft nicht links von der Kippkante liegt, sondern auf der rechten Seite. Half das Gewicht des Würfels bis zu diesem Zeitpunkt immer ein Kippen zu verhindern, so würde es ab diesem Zeitpunkt sogar ein Kippen des Würfels begünstigen. Die Windkraft und die Gewichtskraft erzeugen nun Drehmomente, die versuchen, den Würfel über die kritische Kante zu kippen.
Der Standsicherheitsfaktor
Die Aussage „das Standmoment ist größer als das Kippmoment“ ist in der Technik unbefriedigend. Man möchte nicht nur wissen, ob die Kippgefahr ausgeschlossen ist, sondern auch über welche Reserven die Maschine verfügt. Aus diesem Grund hat man als Bemessungsgrundlage den Standsicherheitsfaktor definiert:
Im ersten Beispiel beträgt der Sicherheitsfaktor ungefähr 1,4:
Beim zweiten Beispiel ist der Standsicherheitsfaktor mit 0,51 kleiner als eins.
Der Standsicherheitsfaktor als Kenngröße hat dabei folgende Bedeutung:
Fall 1: Standsicherheitsfaktor kleiner 1
Es besteht Kippgefahr für die Maschine. Bei den vorliegenden Momenten wir die Maschine umkippen.
Fall 2: Standsicherheitsfaktor von 1
In diesem Fall ist das Kippmoment genauso groß wie das Standmoment: Die Maschine steht „wackelig“ und es kann nicht ausgeschlossen werden, dass sie umkippt. Diese Situation ist für den praktischen Einsatz unbefriedigend.
Fall 3: Standsicherheitsfaktor größer 1
Es besteht keine Kippgefahr für die vorliegende Maschine. Je größer der Standsicherheitsfaktor, desto unwahrscheinlicher ist es, dass die Maschine umkippen wird.
Bei der Berechnung der Standsicherheit von Maschinen sind neben den hier betrachteten statischen Kräften auch dynamische Kräfte, Handkräfte u. v. m. zu berücksichtigen. Die genaue Bestimmung der Standsicherheit unterscheidet sich je nach Maschinentyp und wird in den anzuwendenden Normen beschrieben. Für fahrbare Hubarbeitsbühnen findet man beispielsweise detaillierte Vorgaben in der DIN EN 280.

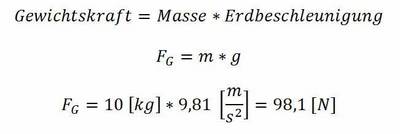
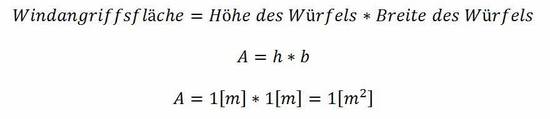

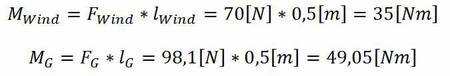
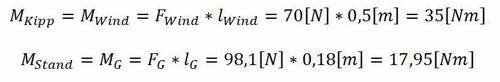
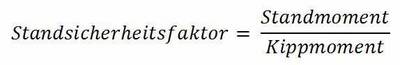
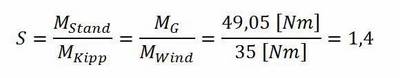

Kommentare (0)
Keine Kommentare gefunden!